Czy zastanawialiście się dlaczego wiele konkurujących ze sobą biznesów działa obok się? Foodtrucki, restauracje, kluby nocne, hotele, lodziarnie, kawiarnie itp. Czy to ma sens? Czy właściciele zarobiliby więcej jakby nie mieli obok konkurenta?
Odpowiedź nie jest taka prosta i szybka. trzeba zapoznać się z podstawami kilku teorii, aby zrozumieć logikę działania takich układów. Długi i być może niełatwy materiał opracował Krzysztof Nosek, ale dla chcących zrozumieć pewne modele biznesowe, ten materiał będzie szybkim ich wyjaśnieniem. Zapraszamy do felietonu.
Każdy mój felieton, artykuł, czy też dłuższą wypowiedź podczas rozmów na tematy branżowe zawsze staram się poprzeć przykładami z własnego doświadczenia. Mówię o tym, co przeżyłem, czego dokonałem z sukcesem, lub czasem (niestety!) z porażką, podaję przykłady z życia wzięte. Uważam, że opisanie czegoś na bazie przebytych doświadczeń jest dużo bardziej wartościowe dla mojego czytelnika czy rozmówcy niż mówienie o suchych faktach wyrwanych z książek, a w myśl zasady „mądry człowiek uczy się na błędach cudzych nie swoich” jest również dużo bardziej twórcze. Dlatego i tym razem odniesiemy się do realiów gastronomicznych z przykładów rynkowych mających odzwierciedlenie w rzeczywistości.
Jakiś czas temu kolega zapytał mnie, czemu często Foodtrucki, restauracje, hotele itp.: są ulokowane tak blisko siebie. Przecież to nie ma sensu?! Nikt nie zarabia? Czy to prawda? Coś w tym jest? Odpowiadając na jego pytanie, żeby nie zanudzić kompana długim wywodem (w końcu spotkaliśmy się powspominać dawne czasy i pomówić o tym, co u kogo słychać, a nie tworzyć monolog akademicki w kawiarni😊) powiedziałem magiczne słowo (najczęściej wykorzystywane chyba w działach prawnych) „TO ZALEŻY”.
Do odpowiedzi na postawione powyżej pytanie przyda się nam pewien wyjątkowy dział matematyki, jakim jest „Teoria gier”. Jest to matematyczna teoria podejmowania decyzji w warunkach konfliktowych opracowana początkowo przez węgierskiego matematyka J. von Neumanna. W teorii tej podmioty, a inaczej mówiąc „gracze” podejmują świadome, logiczne i racjonalne decyzje (strategie), które mają wpływ na ich „położenie”. Żeby lepiej zrozumieć dalsze wywody musimy omówić sobie podstawowe zagadnienia w tej tematyce:
Elementy składowe:
● Gracze – może ich być dwóch lub więcej,
● Strategia – zbiór działań, które wykonują gracze,
● Reguły – najczęściej określane wg warunków rynkowych lub prawnych,
● Wyniki – czy osiągną określony wynik czy też nie,
● Wypłata – korzyści osiągnięte z danego wyniku, najczęściej przedstawiane w formie „macierzy wypłat”.
Rodzaje gier:
● gry – dla dwóch lub więcej osób,
● gry kooperatywne – gracze mogą mieć relację ze sobą i mogą zawierać „koalicje”,
● gry o sumie zerowej- jeden z graczy otrzymuje dokładnie tyle, ile drugi gracz musi oddać,
● gry strategiczne – gracze podejmują swoje decyzje równocześnie,
● gry ekstensywne – decyzje podejmowane są na przemian,
● inne…
Do wyjaśnieniu naszego problemu będzie nam jeszcze potrzebne jedno ważne zagadnienie z teorii gier, a mianowicie „Równowaga Nasha”. Termin ten pochodzi od amerykańskiego matematyka i ekonomisty Johna Forbesa Nasha Jr. Równowaga Nasha to sytuacja w grze niekooperacyjnej, gdzie żaden z graczy nie może podwyższyć swojej wypłaty przez jednostronną (to znaczy bez zmiany strategii wszystkich innych graczy) zmianę swojej strategii. Bardzo upraszczając można to rozumieć w ten sposób, iż jedna ze stron nic nie zyska zmieniając swoja strategię mając na uwadze, że inne jednostki nie zmienią swojej.
Skoro już znamy podstawowe elementy (należy pamiętać, że omawiamy totalne podstawy tego zagadnienia) możemy przejść do przykładów, które nieco bardziej zaczną nam naświetlać tą tematykę oraz przybliżą nas do odpowiedzi na postawione pytanie. Pierwszym przykładem będzie tzw. „dylemat więźnia” – chyba absolutny klasyk gatunku, który moim zdaniem jest świetnym przykładem na działanie oraz zastosowanie teorii gier w życiu.
Dylemat więźnia – w jednym dniu zatrzymano dwóch więźniów. Marka zatrzymano na gorącym uczynku za sprzedaż narkotyków, Tom został zatrzymany również za sprzedaż narkotyków. Obu Panów przywieziono oddzielnie na posterunek. Umieszczono ich w osobnych pomieszczeniach oraz powiedziano, że przyznanie się do winy daje im tylko rok więzienia. W przypadku, gdy obaj nie przyznają się, zostaną wypuszczeni na wolność. Sytuacja komplikuje się w przypadku, gdy tylko jeden z nich przyzna się do winy. W ten sposób obciąży drugiego, a sam uzyska korzystny wyrok. W takim przypadku ten, który przyznał się otrzyma pół roku więzienia, a drugi aż pięć lat. Macierz wypłat w postaci ilości lat do odsiedzenia w więzieniu przedstawia poniższa tabela.
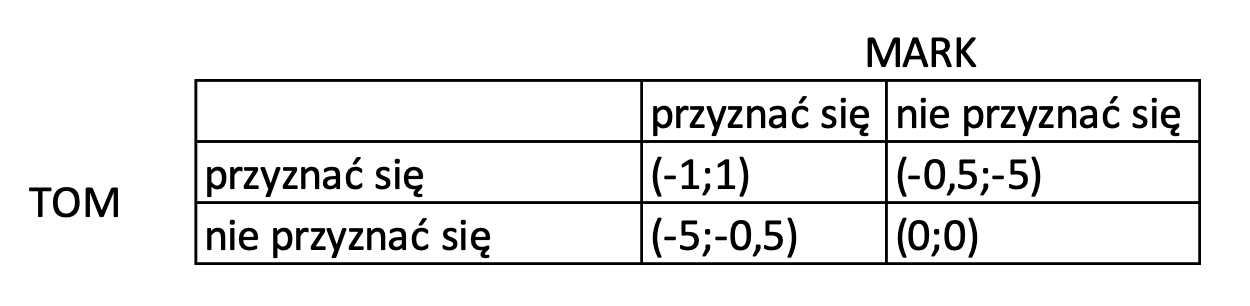
Obserwując macierz wypłat dla Marka i Toma można stwierdzić, że najlepszą decyzję podejmą wtedy, gdy zaprzeczą zarzutom i nie przyznają się do sugerowanego przestępstwa. Jednak żaden z nich nie może mieć pewności, że drugi również się nie przyzna. W przypadku, gdy jeden z nich przyzna się, a drugi nie, wówczas ten drugi traci w grze aż pięć lat w stosunku do sytuacji, kiedy obaj się nie przyznają oraz cztery lata w stosunku do sytuacji, kiedy obaj się przyznają. Zatem najlepszą decyzją, jaką nasi aresztowani powinni podjąć jest przyznanie się. W tej sytuacji po prostu tracą najmniej. I jeżeli obaj podejmą racjonalną decyzję, to wybiorą właśnie tę opcję.
Rozwińmy teraz inny bardzo ciekawy przypadek z życia wzięty, a mianowicie podwyżkę, o jaką może się starać pracownik u swojego pracodawcy. Chyba każdy z nas przynajmniej raz wybrał się, wybiera się lub będzie się wybierał któregoś „pięknego dnia” do swojego przełożonego po tę (zwłaszcza w dzisiejszych czasach) upragnioną podwyżkę wynagrodzenia.
Zobaczmy jak może to wyglądać w przypadku teorii gier:
Na pewno wiecie, że pracodawca prawie zawsze ma przewagę w tej materii, ale teoria gier może to przedstawić w dosadny sposób. Załóżmy, że wyceniacie swoją pracę na 5000 zł netto miesięcznie, podczas gdy firma wycenia was na 3000 zł netto miesięcznie. Mamy więc w teorii przestrzeń do negocjowania w wysokości 2000 zł netto miesięcznie. Firma, jako jedyna strona (nie mówimy tu o ofertach od innych firm, tylko od pracodawcy gdzie jesteście zatrudnieni), która może złożyć propozycję, i zadecyduje czy i ile z tych 2000 zł wam da, a ile zachowa dla siebie. Na przykład firma może zdecydować się na przychylność na waszą korzyść i podzielić się 50/50, tworząc rachunek 1000 zł zł dla was i 1000 zł dla firmy, co oznacza, że wynegocjowane wynagrodzenie wyniesie 4000 zł netto miesięcznie.
Rozważmy strategię w tej grze z perspektywy pracownika. Jeśli pracodawca zaoferuje wam pewną kwotę x , możecie zaakceptować umowę i otrzymać wypłatę w wysokości x . W takim przypadku pracodawca otrzymałby wypłatę w wysokości 2000zł – x . Jeśli jednak odrzucicie ofertę, obaj gracze otrzymają wypłatę zerową, ponieważ nie doszło do zawarcia umowy. No to rozważymy teraz dwa przypadki: kiedy x = 0 i kiedy x > 0. Podsumujmy ten scenariusz za pomocą macierzy wypłat:
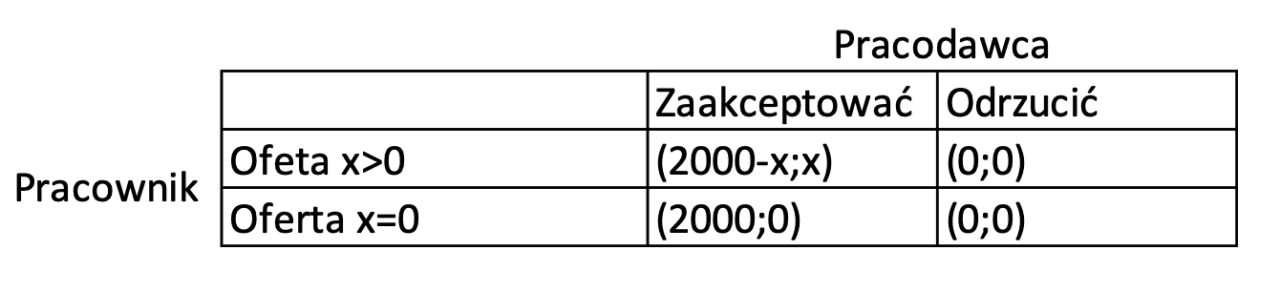
Załóżmy, że zaakceptujecie każdą ofertę jaką przedstawi wam pracodawca. Wtedy najlepszą odpowiedzią pracodawcy jest zaoferowanie 0 zł, co prowadzi do wypłaty 2000 zł dla pracodawcy. Załóżmy teraz, że odrzuciliście transakcję. Oferowanie x > 0 i oferowanie x = 0 są najlepszymi odpowiedziami. Oznacza to, że pracodawca ma dominującą strategię oferowania pracownikowi 0 zł. Niestety to bardzo zła wiadomość dla was jako pracowników! Teoria gier pokazała, że pracodawca nie ma w ogóle motywacji do targowania się, jeśli nie może złożyć kontroferty. I nawet jeśli pracodawca przekazał pracownikowi pewną kwotę x > 0, stanowiąc najlepszą strategię pracownika dotyczącą przyjęcia oferty, x może stanowić maleńki ułamek wynagrodzenia.
Powyższe zadanie pokazuje jak ważne jest rozpisanie sobie macierzy wypłat przed taką rozmową, przeprowadzenie wstępnej symulacji wariantowej oraz określenie swoich mocnych i słabych stron, żeby przewaga negocjacyjna pracodawcy była dużo mniejsza, niż w sytuacji, kiedy pójdziecie po podwyżkę na żywioł z argumentami takimi jak:
● „Pracuję tu 10 lat”
● „Nie spóźniam się”
● „Jestem uczciwy/a”
● „Bardzo dobrze wykonuje swoje obowiązki”
● „Jest inflacja, wszystko drożeje”
● Itp.
Dzięki powyższym przykładom mamy już pewne pojęcie o teorii gier, ale jakie ona może mieć przełożenie na strefę nie biznesową, ale prywatną? To bardzo ciekawe pytanie i nie omieszkam użyć swojego „domowego” przykładu jako odpowiedzi na nie. Jestem zadeklarowanym „wszystkożercą” i jest mi z tym bardzo dobrze. Z kolei moja partnerka jest wegetarianką i jej również jest z tym świetnie. Oboje wiemy, że żadne z nas się nie zmieni i dyskusje nie mają sensu. Niemniej jednak przecież razem wychodzimy, do kawiarni, restauracji, fastfoodów itd. Oczywiście ja, będąc świadomym teorii gier, w głowie szybko rozrysowuję sobie „macierz wypłat” i podejmuje decyzję, co będzie dobrą opcją dla nas dwojga, a jeżeli już nie będzie super dla nas dwojga, to co będzie mniejszym złem dla mnie (drodzy Panowie – to przykład dla was – jesteście teraz świadomi i przygotowani, a waszą maksymą będzie „Jej potencjalna i iluzoryczna racja, a wasz spokój” 😉)
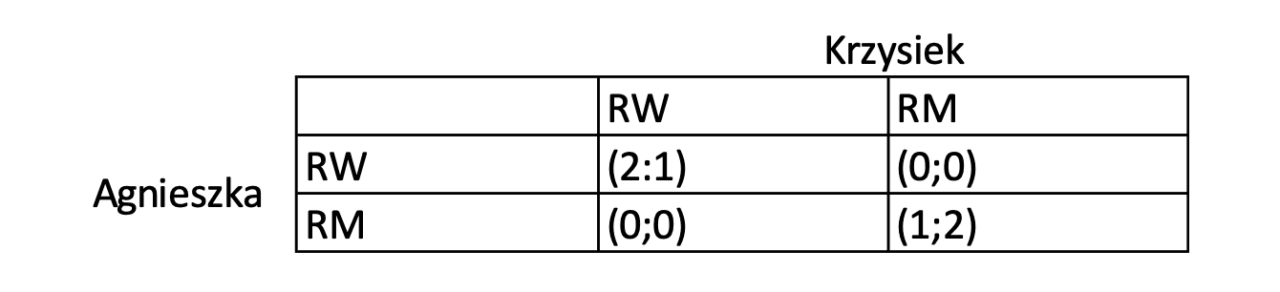
Powyżej prosta macierz wypłat dla dwuosobowej gry o sumie niezerowej. Widać na niej, iż wybranie zarówno przez Agnieszkę jak i Krzysztofa restauracji wege (RW) spowoduje wygraną Agnieszki i mniejszą Krzysztofa. Dlaczego? Agnieszka nie ma obaw, że niczego nie zje w restauracji, bo nie będzie nic dla niej. Krzysztof je wszystko, więc jeden wieczór przeżyje bez mięsa, a spędzi czas razem z partnerką inaczej niż przed TV na kanapie, dlatego też jest po części wygranym. Jeżeli nie będzie konsensusu, Agnieszka wybierze RW, a Krzysztof RM, to się nie spotkają i oboje spędzą osobno wieczory złoszcząc się na siebie i po części również psując sobie humory. Natomiast jeżeli oboje pójdą do restauracji mięsnej (RM), to Agnieszka będzie mieć ograniczony wybór. Nawet jeśli będzie trochę niezadowolona, w najgorszym wypadku zje sałatkę i spędzi czas z Krzysztofem znowu inaczej niż przed TV i na kanapie, dlatego w mniejszym stopniu wygra, a Krzysztof będzie w pełni wygranym.
Przykład z mojego życia był dość trywialny, jak na powagę tematu, ale jego zadaniem było pokazanie, iż wszystko można w ten sposób rozpisać, a ilość strategii może być mnoga (mimo że do tej pory cały czas podawaliśmy zaledwie dwie). Finalnie trzeba zapamiętać, iż teorię gier można stosować praktycznie wszędzie, a przy dobrze zgłębionej tematyce można naprawdę wybitnie przeanalizować problem i wyciągnąć z niego najlepsze z możliwych rozwiązań dające najwięcej korzyści.
No dobrze, a co z pytaniem z początku naszego felietonu?, „…czemu często Foodtrucki, restauracje, hotele itp. bywają ulokowane tak blisko siebie?”. Już spieszę z odpowiedzią.
Skoro już mamy totalne podstawy teorii gier, to do odpowiedzi wykorzystamy model Hotellinga, pochodzący od jego twórcy Harolda Hotellinga – amerykańskiego statystyka i ekonomisty, który opublikował swój wywód w artykule „Stability in Competition’”. Model ten wyjaśnia dlaczego firmy decydują się posiadać swoje jednostki blisko siebie, mimo zwiększonej konkurencji i groźby niższych przychodów. Z racji, że jakiś czas temu pracowałem nad morzem, a wspomnienia i doświadczenia zebrane z tamtego regionu i czasu są mi bardzo bliskie, przykład do wyjaśnienia tego modelu oprzemy na „wózku z lodami na plaży” – pamiętajmy, że to idealny model, bo życie jest trochę bardziej skomplikowane – zawiera prawo, przetargi, strefy graniczne, czynnik ludzki etc. niemniej jednak będzie to bardzo dobry przykład w moim mniemaniu.
Wyobraźmy teraz sobie sprzedawcę Krzyśka (kolorowy wózek), który sprzedaje lody na plaży. Plaża ma tysiąc metrów długości (żeby łatwiej się liczyło), a Krzysiek aktualnie nie ma konkurencji – cóż za idealny model, nieprawdaż? 😊 Krzysiek najprawdopodobniej zlokalizuje swój kolorowy wózek z lodami na środku plaży, gdyż klienci z każdej strony będą mieli do niego po 500m i z łatwością będą mogli kupić w upalne dni lody, dzięki czemu nasz przedsiębiorca obsłuży całą plażę. Nie mniej jednak rynek nie znosi próżni i pojawia się konkurencja – drugi sprzedawca lodów Tomasz (czarny wózek), który chce sprzedawać te same lody na tej samej plaży co Krzysiek. Poniżej zaprezentowałem trzy scenariusze, w których Krzysiek i Tomasz mogą zlokalizować swoje wózki oraz jakie mają możliwe strategie w takim wariancie.
Scenariusz nr 1 – Najlepszy

Źródło: opracowanie własne
Scenariusz nr 1- obaj sprzedawcy umówili się, żeby podzielić plażę dokładnie na pół. Dzięki temu klienci nie muszą chodzić daleko, bo wózki Krzyśka i Tomasza rozstawiono w pierwszej oraz ostatniej ćwiartce plaży. Dzięki temu klienci nie potrzebują więcej niż 250m żeby zaspokoić swoje lodowe potrzeby w upalne dni. Dzięki temu rozwiązaniu obaj Panowie podzielą się po 50% udziału w „rynku”, jeśli chodzi o przychody. Takie rozwiązanie nazywamy „socially optimal solution” (S.O.S).
Scenariusz nr 2 – Zły

Źródło: opracowanie własne
Scenariusz nr 2 – Krzyśkowi nie spodobało się, że Tomasz wszedł na jego terytorium, przez co postanowił przesunąć swój wózek do ostatniej ćwiartki plaży, gdzie sprzedawał Tomasz. Niestety poprzez tę decyzję niektórzy klienci potrzebują teraz aż 750m, aby móc kupić lody. Istnieje bardzo wysokie prawdopodobieństwo, że 75% klientów kupi teraz lody od pierwszego napotkanego sprzedawcy, którym w tym momencie jest Krzysiek, a zaledwie 25% plażowiczów postanowi kupić od Tomasza.
Scenariusz nr 3 – Taka jest rzeczywistość

Źródło: opracowanie własne
Scenariusz nr 3 – Krzysiek oraz Tomasz przesunęli się na środek plaży stając naprzeciw siebie niczym na pojedynku. Teraz żaden ze sprzedawców nie zmieni swojej pozycji, ponieważ jeśli ktoś przesunie się w lewo lub w prawo, straci na swoich klientach i będzie miał mniej niż połowę klientów. Każdy z nich obsługuje teraz 50% konsumentów. Patrząc na ich obecną sytuację osiągnęli tzw. „równowagę Nasha”, gdyż ani Krzysiek ani Tomasz nie może poprawić swojego stanu, odchodząc od obecnej strategii. Jeżeli Krzysiek i Tomasz podzieliliby plażę równo, tak jak na w scenariuszu 1, nadal mieliby taką samą sprzedaż, ale klienci mieliby maksymalnie 250 m do przejścia. Niestety scenariusz 1 jest nie do utrzymania, ze względu na to, że każdy sprzedawca jest zmotywowany do przejęcia większej części rynku, nie zawsze wykazując przy tym logikę oraz sensowność. Strategia obu Panów, żeby znajdować się pośrodku początku oraz końca plaży nie przetrwała (mimo że w obu przypadkach mają taką samą liczbę klientów), ze względu na to, iż nie była to równowaga Nasha. Problem teraz polega na tym, że nie ma już sytuacji S.O.S, a klienci wracają do konieczności chodzenia 500m, aby kupić lody. Dokładnie tak samo, jak wtedy, gdy Krzysiek był jedynym monopolistycznym sprzedawcą.
Każdy z nas widzi w codziennym życiu wiele podobnych biznesów ulokowanych koło siebie tj:
● Stacje benzynowe,
● Restauracje fastfood
● Hotele
● Itp.
Ten jakże prosty felieton daje nam obraz na jeden z powodów, dla których konkurenci często decydują się na wspólną lokalizację. Trzeba pamiętać, że nie jest to jedyny powód, a mogą być inne tj: dostęp do podaży, dostępność pracowników, koszty najmu, siła nabywcza klienta itd. Wszystko to prowadzi do istnienia centralnych obszarów rynku. W prawdziwym świecie klienci przychodzą na te same ulice, bulwary, centra food courtów, obszary rynków itp., dzięki czemu każda firma ma taką samą szansę na sprzedaż swoich produktów oraz pozyskanie udziału w przychodach rynku. Dzięki temu firmy mogą swobodnie konkurować strategiami marketingowymi, różnicując cechy swoich produktów, wprowadzając nowe funkcje produktów, promocje, zachęcać rabatami cenowymi czy programikami lojalnościowymi. Dzięki teorii gier można pomóc sobie podczas wyszukiwania optymalnej lokalizacji dla swojego biznesu, jak również przeanalizować swoich konkurentów.
Czy warto zatem grać? Każdy z nas codziennie rozgrywa przynajmniej kilka gier, nawet jeśli nie robi tego świadomie. Na pewno ta dziedzina może nam pomóc w wielu aspektach naszego życia tj:
● Otwarcie nowego biznesu,
● Skalowanie istniejącego biznesu,
● Inwestycje na rynkach kapitałowych,
● Pomoc przy zmianie pracy,
● Pomoc w uzyskaniu awansu czy podwyżki,
● Strategia podczas prowadzenia wojen – oby jak najmniej ich było w naszym życiu!!!!
● Oraz wielu innych sferach życia społeczno-biznesowego…
Teoria gier nie jest również lekarstwem na wszystkie nasze problemy, nie rozwiąże za nas wszystkich podstawowych zadań czy problemów, ale może nam bardzo pomóc w podjęciu najbardziej racjonalnej z możliwych decyzji i pokazać, jakie mogą wystąpić z tego korzyści. Trzeba również pamiętać o podstawowej zasadzie, która mówi, że „Gracze” zachowują się logicznie i racjonalnie. Dlatego jeżeli mamy świadomość, że nasz przeciwnik jest „szalony” to każda nasza strategia będzie bezużyteczna, ze względu na nasze zachowanie w niej logiki, a u przeciwnika jej braku. Posiadając teraz podstawową wiedzę teoretyczną, możemy w pewnym stopniu zwiększyć nasze szanse na wygraną.
„Nie ma idealnego czasu na start. Nie musisz wiedzieć wszystkiego, żeby zacząć. Po prostu wejdź do gry. Nauczysz się robiąc.”— Jack Canfield
WAŻNE!
Wszystkie treści zawarte w tym felietonie mają wyłącznie charakter informacyjny i edukacyjny. Decyzje podjęte na ich podstawie podejmowane są na wyłączną odpowiedzialność czytającego. Zawarte w felietonie dane, opracowania, informacje, analizy zostały przygotowane wyłącznie w celach informacyjnych, są tylko i wyłącznie subiektywnymi opiniami autora.

O autorze:
Krzysztof Nosek jest związany z branżą gastronomiczną od 15 lat. Posiada również wszechstronne wykształcenie z zakresu gastronomii, ekonomii, finansów, jest również absolwentem studiów MBA. Doświadczenie zdobywał w różnych obszarach HoReCa, zarówno w hotelach sieciowych, jak i w obiektach niezależnych za granicą (min. Dion Palace, Grecian Sands) oraz w Polsce (m.in. w Zamku Kliczków, Pałacu Bonerowskim, Marine Hotel, Hotel Mazurkas & Mazurkas Catering 360). Przeszedł całą ścieżkę awansów – poczynając od kelnera, przez kierownika zmiany do stanowisk dyrektorskich. Odpowiadał za zarządzanie personelem, a także brał aktywny udział w ustalaniu i realizacji strategii rozwoju obiektów oraz tworzeniu nowych produktów sprzedażowych. Jego wszechstronna wiedza z zakresu gastronomii, prawa, modelowania finansowego, controllingu, działań operacyjnych oraz analitycznych pozwoliła mu zająć stanowiska dyrektora analiz czy dyrektora controllingu w znanych sieciach gastronomicznych. Do licznych sukcesów Krzysztofa Noska można zaliczyć obsługę głów Państw wg protokołu dyplomatycznego, tj. Prezydenta, Premiera i Ministrów RP, prowadzenie zespołów, wraz z którymi zdobywał liczne nagrody i wyróżnienia w konkursach (m.in. Wine and Food Noble Night, food business awards, „Polska od kuchni – złoty widelec”) oraz implementację wielu własnych pomysłów, działań umożliwiających rozwój podległych obiektów.












![[WAŻNE] PKD wchodzące do Tarczy Finansowej PFR 2.0 – oficjalne wytyczne](https://www.horecabc.pl/wp-content/uploads/2020/11/PFR-100x70.jpg)

